Algorithmic efficiency
In computer science, efficiency is used to describe properties of an algorithm relating to how much of various types of resources it consumes. Algorithmic efficiency can be thought of as analogous to engineering productivity for a repeating or continuous process, where the goal is to reduce resource consumption, including time to completion, to some acceptable, optimal level.
No automatic process
Gregory Chaitin proved that compacting an algorithm cannot be automated by a generalized algorithm;[1] rather, it can only be done heuristically, i.e. by exhaustive search (examples to be found at Busy beaver), trial and error, cleverness, insight, application of inductive reasoning, etc.
Software metrics
The two most frequently encountered and measurable metrics of an algorithm are:-
- speed or running time - the time it takes for an algorithm to complete, and
- 'space' - the memory or 'non-volatile storage' used by the algorithm during its operation.
but also might apply to
- transmission size - such as required bandwidth during normal operation or
- size of external memory- such as temporary disk space used to accomplish its task
and perhaps even
- the size of required 'longterm' disk space required after its operation to record its output or maintain its required function during its required useful lifetime (examples: a data table, archive or a computer log) and also
- the performance per watt and the total energy, consumed by the chosen hardware implementation (with its System requirements, necessary auxiliary support systems including interfaces, cabling, switching, cooling and security), during its required useful lifetime. See Total cost of ownership for other potential costs that might be associated with any particular implementation.
(An extreme example of these metrics might be to consider their values in relation to a repeated simple algorithm for calculating and storing (π+n) to 50 decimal places running for say, 24 hours, on a processor operating in its own purpose-built heated or air conditioned unit.)
The process of making code more efficient is known as optimization and in the case of automatic optimization (i.e. compiler optimization - performed by compilers on request or by default), usually focus on space at the cost of speed, or vice versa. There are also quite simple programming techniques and 'avoidance strategies' that can actually improve both at the same time, usually irrespective of hardware, software or language. Even the re-ordering of nested conditional statements to put the least frequently occurring condition first can reduce actual instruction path length. For example, a condition might test patients for (age > 18) before testing (blood type == 'AB-') because this type of blood occurs in only about 1 in 100 of the population. This would eliminate the second test at runtime in 99% of instances; something an optimizing compiler would almost certainly not be aware of - but which a programmer can research relatively easily even without specialist medical knowledge.
History
The first machines that were capable of computation were severely limited by purely mechanical considerations. As later electronic machines were developed they were, in turn, limited by the speed of their electronic counterparts. As software replaced hard-wired circuits, the efficiency of algorithms also became important. It has long been recognized that the precise 'arrangement of processes' is critical in reducing elapse time.
-
"In almost every computation a great variety of arrangements for the succession of the processes is possible, and various considerations must influence the selections amongst them for the purposes of a calculating engine. One essential object is to choose that arrangement which shall tend to reduce to a minimum the time necessary for completing the calculation"
-
- Ada Lovelace 1815-1852, generally considered as 'the first programmer' who worked on Charles Babbage's early mechanical general-purpose computer
-
"In established engineering disciplines a 12% improvement, easily obtained, is never considered marginal and I believe the same viewpoint should prevail in software engineering"[2]
-
- Extract from "Structured Programming with go to Statements" by Donald Knuth, renowned computer scientist and Professor Emeritus of the Art of Computer Programming[3] at Stanford University.
-
"The key to performance is elegance, not battalions of special cases"
-
- attributed to Jon Bentley and (Malcolm) Douglas McIlroy
Speed
The absolute speed of an algorithm for a given input can simply be measured as the duration of execution (or clock time) and the results can be averaged over several executions to eliminate possible random effects. Most modern processors operate in a multi-processing & multi-programming environment so consideration must be made for parallel processes occurring on the same physical machine, eliminating these as far as possible. For superscalar processors, the speed of a given algorithm can sometimes be improved through instruction-level parallelism within a single processor (but, for optimal results, the algorithm may require some adaptation to this environment to gain significant advantage ('speedup'), becoming, in effect, an entirely different algorithm). A relative measure of an algorithms performance can sometimes be gained from the total instruction path length which can be determined by a run time Instruction Set Simulator (where available).
An estimate of the speed of an algorithm can be determined in various ways. The most common method uses time complexity to determine the Big-O of an algorithm. See Run-time analysis for estimating how fast a particular algorithm may be according to its type (example: lookup unsorted list, lookup sorted list etc.) and in terms of scalability - its dependence on 'size of input', processor power and other factors.
Memory
Often, it is possible to make an algorithm faster at the expense of memory. This might be the case whenever the result of an 'expensive' calculation is cached rather than recalculating it afresh each time. The additional memory requirement would, in this case, be considered additional overhead although, in many situations, the stored result occupies very little extra space and can often be held in pre-compiled static storage, reducing not just processing time but also allocation & deallocation of working memory. This is a very common method of improving speed, so much so that some programming languages often add special features to support it, such as C++'s 'mutable' keyword.
The memory requirement of an algorithm is actually two separate but related things:-
- The memory taken up by the compiled executable code (the object code or binary file) itself (on disk or equivalent, depending on the hardware and language). This can often be reduced by preferring run-time decision making mechanisms (such as virtual functions and run-time type information) over certain compile-time decision making mechanisms (such as macro substitution and templates). This, however, comes at the cost of speed.
- Amount of temporary "dynamic memory" allocated during processing. For example, dynamically pre-caching results, as mentioned earlier, improves speed at the cost of this attribute. Even the depth of sub-routine calls can impact heavily on this cost and increase path length too, especially if there are 'heavy' dynamic memory requirements for the particular functions invoked. The use of copied function parameters (rather than simply using pointers to earlier, already defined, and sometimes static values) actually doubles the memory requirement for this particular memory metric (as well as carrying its own processing overhead for the copying itself. This can be particularly relevant for quite 'lengthy' parameters such as html script, JavaScript source programs or extensive freeform text such as letters or emails.
(See also sections Choice of instruction or data type and Avoiding costs concerning deliberate 'stretching' of data structures to force them to have a fixed length which then becomes a multiple of 2, 4, 8 etc.)
Rematerialization
It has been argued that Rematerialization (re-calculating) may occasionally be more efficient than holding results in cache. This is the somewhat non-intuitive belief that it can be faster to re-calculate from the input - even if the answer is already known - when it can be shown, in some special cases, to decrease "register pressure". Some optimizing compilers have the ability to decide when this is considered worthwhile based on a number of criteria such as complexity and no side effects, and works by keeping track of the expression used to compute each variable, using the concept of available expressions.
This is most likely to be true when a calculation is very fast (such as addition or bitwise operations), while the amount of data which must be cached would be very large, resulting in inefficient storage. Small amounts of data can be stored very efficiently in registers or fast cache, while in most contemporary computers large amounts of data must be stored in slower memory or even slower hard drive storage, and thus the efficiency of storing data which can be computed quickly drops significantly.
Precomputation
Precomputing a complete range of results prior to compiling, or at the beginning of an algorithm's execution, can often increase algorithmic efficiency substantially. This becomes advantageous when one or more inputs is constrained to a small enough range that the results can be stored in a reasonably sized block of memory. Because memory access is essentially constant in time complexity (except for caching delays), any algorithm with a component which has worse than constant efficiency over a small input range can be improved by precomputing values. In some cases efficient approximation algorithms can be obtained by computing a discrete subset of values and interpolating for intermediate input values, since interpolation is also a linear operation.
Transmission size
Data compression algorithms can be useful because they help reduce the consumption of expensive resources, such as hard disk space or transmission bandwidth. This however also comes at a cost - which is additional processing time to compress and subsequently decompress. Depending upon the speed of the data transfer, compression may reduce overall response times which, ultimately, equates to speed - even though processing within the computer itself takes longer. For audio, MP3 is a compression method used extensively in portable sound systems. The efficiency of a data compression algorithm relates to the compression factor and speed of achieving both compression and decompression. For the purpose of archiving an extensive database, it might be considered worthwhile to achieve a very high compression ratio, since decompression is less likely to occur on the majority of the data.
Data presentation
Output data can be presented to the end user in many ways - such as via punched tape or card, digital displays, local display monitors, remote computer monitors or printed. Each of these has its own inherent initial cost and, in some cases, an ongoing cost (e.g. refreshing an image from memory) . As an example, the web site "Google" recently showed, as its logo,[4] an image of the Vancouver olympics that is around 8K of gif image.[5] The normally displayed Google image is a PNG image of 28K (or 48K), yet the raw text string for "Google" occupies only 6 octets or 48 bits (4,778 or 8192 times less). This graphically illustrates that how data is presented can significantly effect the overall efficiency of transmission (and also the complete algorithm - since both GIF and PNG images require yet more processing).
It is estimated by "Internet World Stats" [6] that there were 1,733,993,741 internet users in 2009 and, to transmit this new image to each one of them, would require around 136,000 billion (109)octets of data to be transmitted - at least once - into their personal web cache.[7] In "Computational Energy Cost of TCP",[7] co-authors Bokyung Wang and Suresh Singh examine the energy costs for TCP and calculated, for their chosen example, a cost of 0.022 Joules per packet (of approx 1489 octets). On this basis, a total of around 2,000,000,000 joules (2 GJ) of energy might be expended by TCP elements alone to display the new logo for all users for the first time. To maintain or re-display this image requires still more processing and consequential energy cost (in contrast to printed output for instance).
Encoding and decoding methods (compared and contrasted)
When data is encoded for any 'external' use, it is possible to do so in an almost unlimited variety of different formats that are sometimes conflicting. This content encoding (of the raw data) may be designed for:
- optimal readability – by humans
- optimal decoding speed – by other computer programs
- optimal compression – for archiving or data transmission
- optimal compatibility – with "legacy" or other existing formats or programming languages
- optimal security – using encryption
(For character level encoding, see the various encoding techniques such as EBCDIC or ASCII )
It is unlikely that all of these goals could be met with a single 'generic' encoding scheme and so a compromise will often be the desired goal and will often be compromised by the need for standardization and/or legacy and compatibility issues.
Encoding efficiently
For data encoding whose destination is to be input for further computer processing, readability is not an issue – since the receiving processors algorithm can decode the data to any other desirable form including human readable. From the perspective of algorithmic efficiency, minimizing subsequent decoding (with zero or minimal parsing) should take highest priority. The general rule of thumb is that any encoding system that 'understands' the underlying data structure - sufficiently to encode it in the first place - should be equally capable of easily encoding it in such a way that makes decoding it highly efficient. For variable length data with possibly omitted data values, for instance, this almost certainly means the utilization of declarative notation (i.e. including the length of the data item as a prefix to the data so that a de-limiter is not required and parsing completely eliminated). For keyword data items, tokenizing the key to an index (integer) after its first occurrence not only reduces subsequent data size but, furthermore, reduces future decoding overhead for the same items that are repeated.
For more 'generic' encoding for efficient data compression see Arithmetic encoding and entropy encoding articles.
Historically, optimal encoding was not only worthwhile from an efficiency standpoint but was also common practise to conserve valuable memory, external storage and processor resources. Once validated a country name for example could be held as a shorter sequential country code which could then also act as an index for subsequent 'decoding', using this code as an entry number within a table or record number within a file. If the table or file contained fixed length entries, the code could easily be converted to an absolute memory address or disk address for fast retrieval. The ISBN system for identifying books is a good example of a practical encoding method which also contains a built-in hierarchy.
According to recent articles in New Scientist[8] and Scientific American;[9] "TODAY'S telecommunications networks could use one ten-thousandth of the power they presently consume if smarter data-coding techniques were used", according to Bell Labs, based in Murray Hill, New Jersey It recognizes that this is only a theoretical limit but nevertheless sets itself a more realistic, practical goal of a 1,000 fold reduction within 5 years with future, as yet unidentified, technological changes.[10]
Examples of several common encoding methods
- Comma separated values (CSV - a list of data values separated by commas)
- Tab separated values (TSV) - a list of data values separated by 'tab' characters
- HyperText Markup Language (HTML) - the predominant markup language for web pages
- Extensible Markup Language (XML) - a generic framework for storing any amount of text or any data whose structure can be represented as a tree with at least one element - the root element.
- JavaScript Object Notation (JSON) - human-readable format for representing simple data structures
The last of these, (JSON) is apparently widely used for internet data transmission, primarily it seems because the data can be uploaded by a single JavaScript 'eval' statement - without the need to produce what otherwise would likely have been a more efficient purpose built encoder/decoder. There are in fact quite large amounts of repeated (and therefore redundant data) in this particular format, and also in HTML and XML source, that could quite easily be eliminated. XML is recognized as a verbose form of encoding.[11] Binary XML has been put forward as one method of reducing transfer and processing times for XML and, while there are several competing formats, none has been widely adopted by a standards organization or accepted as a de facto standard.[12] It has also been criticized by Jimmy Zhang for essentially trying to solve the wrong problem[13]
There are a number of freely available products on the market that partially compress HTML files and perform some or all of the following:
- merge lines
- remove unnecessary whitespace characters
- remove unnecessary quotation marks. For example, BORDER="0" will be replaced with BORDER=0)
- replace some tags with shorter ones (e.g. replace STRIKE tags with S, STRONG with B and EM with I)
- remove HTML comments (comments within scripts and styles are not removed)
- remove <!DOCTYPE..> tags
- remove named meta tags
The effect of this limited form of compression is to make the HTML code smaller and faster to load, but more difficult to read manually (so the original HTML code is usually retained for updating), but since it is predominantly meant to be processed only by a browser, this causes no problems. Despite these small improvements, HTML, which is the predominant language for the web still remains a predominantly source distributed, interpreted markup language, with high redundancy.
Kolmogorov complexity
The study of encoding techniques has been examined in depth in an area of computer science characterized by a method known as Kolmogorov complexity where a value known as ('K') is accepted as 'not a computable function'. The Kolmogorov complexity of any computable object is the length of the shortest program that computes it and then halts. The invariance theorem shows that it is not really important which computer is used. Essentially this implies that there is no automated method that can produce an optimum result and is therefore characterized by a requirement for human ingenuity or Innovation. See also Algorithmic probability.
Effect of programming paradigms
The effect that different programming paradigms have on algorithmic efficiency is fiercely contested, with both supporters and antagonists for each new paradigm. Strong supporters of structured programming, such as Dijkstra for instance, who favour entirely goto-less programs are met with conflicting evidence that appears to nullify its supposed benefits.[14] The truth is, even if the structured code itself contains no gotos, the optimizing compiler that creates the binary code almost certainly generates them (and not necessarily in the most efficient way). Similarly, OOP protagonists who claim their paradigm is superior are met with opposition from strong sceptics such as Alexander Stepanov who suggested that OOP provides a mathematically limited viewpoint and called it, "almost as much of a hoax as Artificial Intelligence" [15][16][17] In the long term, benchmarks, using real-life examples, provide the only real hope of resolving such conflicts - at least in terms of run-time efficiency.
Optimization techniques
The word optimize is normally used in relation to an existing algorithm/computer program (i.e. to improve upon completed code). In this section it is used both in the context of existing programs and also in the design and implementation of new algorithms, thereby avoiding the most common performance pitfalls. It is clearly wasteful to produce a working program - at first using an algorithm that ignores all efficiency issues - only to then have to redesign or rewrite sections of it if found to offer poor performance. Optimization can be broadly categorized into two domains:-
- Environment specific - that are essentially worthwhile only on certain platforms or particular computer languages
- General techniques - that apply irrespective of platform
Environment specific
Optimization of algorithms frequently depends on the properties of the machine the algorithm will be executed on as well as the language the algorithm is written in and chosen data types. For example, a programmer might optimize code for time efficiency in an application for home computers (with sizable amounts of memory), but for code destined to be embedded in small, "memory-tight" devices, the programmer may have to accept that it will run more slowly, simply because of the restricted memory available for any potential software optimization.
For a discussion of hardware performance, see article on Computer performance which covers such things as CPU clock speed, cycles per instruction and other relevant metrics. For a discussion on how the choice of particular instructions available on a specific machine effect efficiency, see later section 'Choice of instruction and data type'.
General techniques
- Linear search such as unsorted table look-ups in particular can be very expensive in terms of execution time but can be reduced significantly through use of efficient techniques such as indexed arrays and binary searches. Using a simple linear search on first occurrence and using a cached result thereafter is an obvious compromise.
- Use of indexed program branching, utilizing branch tables or "threaded code" to control program flow, (rather than using multiple conditional IF statements or unoptimized CASE/SWITCH) can drastically reduce instruction path length, simultaneously reduce program size and even also make a program easier to read and more easily maintainable (in effect it becomes a 'decision table' rather than repetitive spaghetti code).
- Loop unrolling performed manually, or more usually by an optimizing compiler, can provide significant savings in some instances. By processing 'blocks' of several array elements at a time, individually addressed, (for example, within a
Whileloop), much pointer arithmetic and end of loop testing can be eliminated, resulting in decreased instruction path lengths. Other Loop optimizations are also possible.
Tunnel vision
There are many techniques for improving algorithms, but focusing on a single favorite technique can lead to a "tunnel vision" mentality. For example, in this[18] X86 assembly example, the author offers loop unrolling as a reasonable technique that provides some 40% improvements to his chosen example. However, the same example would benefit significantly from both inlining and use of a trivial hash function. If they were implemented, either as alternative or complementary techniques, an even greater percentage gain might be expected. A combination of optimizations may provide ever increasing speed, but selection of the most easily implemented and most effective technique, from a large repertoire of such techniques, is desirable as a starting point.
Dependency trees and spreadsheets
Spreadsheets are a 'special case' of algorithms that self-optimize by virtue of their dependency trees that are inherent in the design of spreadsheets to reduce re-calculations when a cell changes. The results of earlier calculations are effectively cached within the workbook and only updated if another cells changed value effects it directly.
Table lookup
Table lookups can make many algorithms more efficient, particularly when used to bypass computations with a high time complexity. However, if a wide input range is required, they can consume significant storage resources. In cases with a sparse valid input set, hash functions can be used to provide more efficient lookup access than a full table.
Hash function algorithms
A hash function is any well-defined procedure or mathematical function which converts a large, possibly variable-sized amount of data into a small datum, usually a single integer that may serve as an index to an array. The values returned by a hash function are called hash values, hash codes, hash sums, or simply hashes.
Hash functions are frequently used to speed up table lookups. The choice of a hashing function (to avoid a linear or brute force search) depends critically on the nature of the input data, and their probability distribution in the intended application.
Trivial hash function
Sometimes if the datum is small enough, a "trivial hash function" can be used to effectively provide constant time searches at almost zero cost. This is particularly relevant for single byte lookups (e.g. ASCII or EBCDIC characters)
Searching strings
Searching for particular text strings (for instance "tags" or keywords) in long sequences of characters potentially generates lengthy instruction paths. This includes searching for delimiters in comma separated files or similar processing which can be very simply and effectively eliminated (using declarative notation for instance).
Several methods of reducing the cost for general searching have been examined and the "Boyer–Moore string search algorithm" (or Boyer–Moore–Horspool algorithm, a similar but modified version) is one solution that has been proven to give superior results to repetitive comparisons of the entire search string along the sequence.[19]
Hot spot analyzers
Special system software products known as "performance analyzers" are often available from suppliers to help diagnose "hot spots" - during actual execution of computer programs - using real or test data - they perform a Performance analysis under generally repeatable conditions.[20] They can pinpoint sections of the program that might benefit from specifically targeted programmer optimization without necessarily spending time optimizing the rest of the code. Using program re-runs, a measure of relative improvement can then be determined to decide if the optimization was successful and by what amount. Instruction Set Simulators can be used as an alternative to measure the instruction path length at the machine code level between selected execution paths, or on the entire execution.
Regardless of the type of tool used, the quantitative values obtained can be used in combination with anticipated reductions (for the targeted code) to estimate a relative or absolute overall saving. For example if 50% of the total execution time (or path length) is absorbed in a subroutine whose speed can be doubled by programmer optimization, an overall saving of around 25% might be expected (Amdahl law).
Efforts have been made at the University of California, Irvine to produce dynamic executable code using a combination of hot spot analysis and run-time program trace tree. A JIT like dynamic compiler was built by Andreas Gal and others, "in which relevant (i.e., frequently executed) control flows are ...discovered lazily during execution"[21]
Benchmarking & competitive algorithms
For new versions of software or to provide comparisons with competitive systems, benchmarks are sometimes used which assist with gauging an algorithms relative performance. If a new sort algorithm is produced for example it can be compared with its predecessors to ensure that at least it is efficient as before with known data - taking into consideration any functional improvements. Benchmarks can be used by customers when comparing various products from alternative suppliers to estimate which product will best suit their specific requirements in terms of functionality and performance. For example in the mainframe world certain proprietary sort products from independent software companies such as Syncsort compete with products from the major suppliers such as IBM for speed. Some benchmarks provide opportunities for producing an analysis comparing the relative speed of various compiled and interpreted languages for example[22][23] and The Computer Language Benchmarks Game[24] compares the performance of implementations of typical programming problems in several programming languages. (Even creating "do it yourself" benchmarks to get at least some appreciation of the relative performance of different programming languages, using a variety of user specified criteria, is quite simple to produce as this "Nine language Performance roundup" by Christopher W. Cowell-Shah demonstrates by example)[25]
Compiled versus interpreted languages
A compiled algorithm will, in general, execute faster than the equivalent interpreted algorithm simply because some processing is required even at run time to 'understand' (i.e. interpret) the instructions to effect an execution. A compiled program will normally output an object or machine code equivalent of the algorithm that has already been processed by the compiler into a form more readily executed by microcode or the hardware directly. The popular Perl language is an example of an interpreted language and benchmarks indicate that it executes approximately 24 times more slowly than compiled C.[23]
Optimizing compilers
Many compilers have features that attempt to optimize the code they generate, utilizing some of the techniques outlined in this article and others specific to the compilation itself. Loop optimization is often the focus of optimizing compilers because significant time is spent in program loops and parallel processing opportunities can often be facilitated by automatic code re-structuring such as loop unrolling. Optimizing compilers are by no means perfect. There is no way that a compiler can guarantee that, for all program source code, the fastest (or smallest) possible equivalent compiled program is output; such a compiler is fundamentally impossible because it would solve the halting problem. Additionally, even optimizing compilers generally have no access to runtime metrics to enable them to improve optimization through 'learning'.
Just-in-time compilers
'On-the-fly' processors known today as just-in-time or 'JIT' compilers combine features of interpreted languages with compiled languages and may also incorporate elements of optimization to a greater or lesser extent. Essentially the JIT compiler can compile small sections of source code statements (or bytecode) as they are newly encountered and (usually) retain the result for the next time the same source is processed. In addition, pre-compiled segments of code can be in-lined or called as dynamic functions that themselves perform equally fast as the equivalent 'custom' compiled function. Because the JIT processor also has access to run-time information (that a normal compiler cannot have) it is also possible for it to optimize further executions depending upon the input and also perform other run-time introspective optimization as execution proceeds. A JIT processor may, or may not, incorporate self modifying code or its equivalent by creating 'fast path' routes through an algorithm. It may also use such techniques as dynamic Fractional cascading or any other similar runtime device based on collected actual runtime metrics. It is therefore entirely possible that a JIT compiler might (counter intuitively) execute even faster than an optimally 'optimized' compiled program.
Self-modifying code
As mentioned above, just-in-time compilers often make extensive use of self-modifying code to generate the actual machine instructions required to be executed. The technique can also be used to reduce instruction path lengths in application programs where otherwise repetitive conditional tests might otherwise be required within the main program flow. This can be particularly useful where a sub routine may have embedded debugging code that is either active (testing mode) or inactive (production mode) depending upon some input parameter. A simple solution using a form of dynamic dispatching is where the sub routine entry point is dynamically 'swapped' at initialization, depending upon the input parameter. Entry point A) includes the debugging code prologue and entry point B) excludes the prologue; thus eliminating all overhead except the initial 'test and swap' (even when test/debugging is selected, when the overhead is simply the test/debugging code itself).
Genetic algorithm
In the world of performance related algorithms it is worth mentioning the role of genetic algorithms which compete using similar methods to the natural world in eliminating inferior algorithms in favour of more efficient versions.
Object code optimizers
Some proprietary program optimizers such as the "COBOL Optimizer" developed by Capex Corporation in the mid-1970s for COBOL, actually took the unusual step of optimizing the Object code (or binary file) after normal compilation. This type of optimizer, recently sometimes referred to as a "post pass" optimizer or peephole optimizer, depended, in this case, upon knowledge of 'weaknesses' in the standard IBM COBOL compiler and actually replaced (or patched) sections of the object code with more efficient code.
A number of other suppliers have recently adopted the same approach. See main article for list of these products
Alignment of data
Most processors execute faster if certain data values are aligned on word, doubleword or page boundaries.[26] If possible design/specify structures to satisfy appropriate alignments. This avoids exceptions.
Locality of reference
To reduce Cache miss exceptions by providing good spatial locality of reference, specify 'high frequency'/volatile working storage data within defined structure(s) so that they are also allocated from contiguous sections of memory (rather than possibly scattered over many pages).[27] Group closely related data values also 'physically' close together within these structures. Consider the possibility of creating an 'artificial' structure to group some otherwise unrelated, but nevertheless frequently referenced, items together.
Choice of instruction or data type
Particularly in an Assembly language (although also applicable to HLL statements), the choice of a particular 'instruction' or data type, can have a large impact on execution efficiency. In general, instructions that process variables such as signed or unsigned 16-bit or 32-bit integers are faster than those that process floating point or packed decimal. Modern processors are even capable of executing multiple 'fixed point' instructions in parallel with the simultaneous execution of a floating point instruction. If the largest integer to be encountered can be accommodated by the 'faster' data type, defining the variables as that type will result in faster execution - since even a non-optimizing compiler will, in-effect, be 'forced' to choose appropriate instructions that will execute faster than would have been the case with data types associated with 'slower' instructions. Assembler programmers (and optimizing compiler writers) can then also benefit from the ability to perform certain common types of arithmetic for instance - division by 2, 4, 8 etc. by performing the very much faster binary shift right operations (in this case by 1, 2 or 3 bits).
If the choice of input data type is not under the control of the programmer, although prior conversion (outside of a loop for instance) to a faster data type carries some overhead, it can often be worthwhile if the variable is then to be used as a loop counter, especially if the count could be quite a high value or there are many input values to process. As mentioned above, choice of individual assembler instructions (or even sometimes just their order of execution) on particular machines can effect the efficiency of an algorithm. See Assembly Optimization Tips for one quite numerous arcane list of various technical (and sometimes non-intuitive) considerations for choice of assembly instructions on different processors that also discusses the merits of each case. Sometimes microcode or hardware quirks can result in unexpected performance differences between processors that assembler programmers can actively code for - or else specifically avoid if penalties result - something even the best optimizing compiler may not be designed to handle.
Data granularity
The greater the granularity of data definitions (such as splitting a geographic address into separate street/city/postal code fields) can have performance overhead implications during processing. Higher granularity in this example implies more procedure calls in Object-oriented programming and parallel computing environments since the additional objects are accessed via multiple method calls rather than perhaps one.
Subroutine granularity
For structured programming and procedural programming in general, great emphasis is placed on designing programs as a hierarchy of (or at least a set of) subroutines. For object oriented programming, the method call (a subroutine call) is the standard method of testing and setting all values in objects and so increasing data granularity consequently causes increased use of subroutines. The greater the granularity of subroutine usage, the larger the proportion of processing time devoted to the mechanism of the subroutine linkages themselves.The presence of a (called) subroutine in a program contributes nothing extra to the functionality of the program. The extent to which subroutines (and their consequent memory requirements) influences the overall performance of the complete algorithm depends to a large extent on the actual implementation.
In assembly language programs, the invocation of a subroutine need not involve much overhead, typically adding just a couple of machine instructions to the normal instruction path length, each one altering the control flow either to the subroutine or returning from it (saving the state on a stack being optional, depending on the complexity of the subroutine and its requirement to reuse general purpose registers). In many cases, small subroutines that perform frequently used data transformations using 'general purpose' work areas can be accomplished without the need to save or restore any registers, including the return register.
By contrast, HLL programs typically always invoke a 'standard' procedure call (the calling convention), which involves saving the program state by default and usually allocating additional memory on the stack to save all registers and other relevant state data (the prologue and epilogue code).[28][29] Recursion in a HLL program can consequently consume significant overhead in both memory and execution time managing the stack to the required depth.
Guy Steele pointed out in a 1977 paper[29] that a well-designed programming language implementation can have very low overheads for procedural abstraction (but laments, in most implementations, that they seldom achieve this in practice - being "rather thoughtless or careless in this regard"). Steele concludes that "we should have a healthy respect for procedure calls" (because they are powerful) but he also cautioned "use them sparingly"[29]
See section Avoiding costs for discussion of how inlining subroutines can be used to improve performance. For the Java language, use of the "final" keyword can be used to force method inlining (resulting in elimination of the method call, no dynamic dispatch and the possibility to constant-fold the value - with no code executed at runtime)[30]
Choice of language / mixed languages
Some computer languages can execute algorithms more efficiently than others. As stated already, interpreted languages often perform less efficiently than compiled languages. In addition, where possible, 'high-use', and time-dependent sections of code may be written in a language such as assembler that can usually execute faster and make better use of resources on a particular platform than the equivalent HLL code on the same platform. This section of code can either be statically called or dynamically invoked (external function) or embedded within the higher level code (e.g. Assembler instructions embedded in a 'C' language program). The effect of higher levels of abstraction when using a HLL has been described as the Abstraction penalty[31][32][33] Programmers who are familiar with assembler language (in addition to their chosen HLL) and are also familiar with the code that will be generated by the HLL, under known conditions, can sometimes use HLL language primitives of that language to generate code almost identical to assembler language. This is most likely to be possible only in languages that support pointers such as PL/1 or C. This is facilitated if the chosen HLL compiler provides an optional assembler listing as part of its printout so that various alternatives can be explored without also needing specialist knowledge of the compiler internals.
Software validation versus hardware validation
An optimization technique that was frequently taken advantage of on 'legacy' platforms was that of allowing the hardware (or microcode) to perform validation on numeric data fields such as those coded in (or converted to) packed decimal (or packed BCD). The choice was to either spend processing time checking each field for a valid numeric content in the particular internal representation chosen or simply assume the data was correct and let the hardware detect the error upon execution. The choice was highly significant because to check for validity on multiple fields (for sometimes many millions of input records), it could occupy valuable computer resources. Since input data fields were in any case frequently built from the output of earlier computer processing, the actual probability of a field containing invalid data was exceedingly low and usually the result of some 'corruption'. The solution was to incorporate an 'event handler' for the hardware detected condition ('data exception)' that would intercept the occasional errant data field and either 'report, correct and continue' or, more usually, abort the run with a core dump to try to determine the reason for the bad data.
Similar event handlers are frequently utilized in today's web based applications to handle other exceptional conditions but repeatedly parsing data input, to ensure its validity before execution, has nevertheless become much more commonplace - partly because processors have become faster (and the perceived need for efficiency in this area less significant) but, predominantly - because data structures have become less 'formalized' (e.g. .csv and .tsv files) or uniquely identifiable (e.g. packed decimal). The potential savings using this type of technique may have therefore fallen into general dis-use as a consequence and therefore repeated data validations and repeated data conversions have become an accepted overhead. Ironically, one consequence of this move to less formalized data structures is that a corruption of say, a numeric binary integer value, will not be detected at all by the hardware upon execution (for instance: is an ASCII hexadecimal value '20202020' a valid signed or unsigned binary value - or simply a string of blanks that has corrupted it?)
Algorithms for vector & superscalar processors
Algorithms for vector processors are usually different than those for scalar processors since they can process multiple instructions and/or multiple data elements in parallel (for examples of these differences see 'description' in the main article). The process of converting an algorithm from a scalar to a vector process is known as vectorization and methods for automatically performing this transformation as efficiently as possible are constantly sought. There are intrinsic limitations for implementing instruction level parallelism in Superscalar processors (which are discussed in the 'limitations' section in the main article) but, in essence, the overhead in deciding for certain if particular instruction sequences can be processed in parallel can sometimes exceed the efficiency gain in so doing. The achievable reduction is governed primarily by the (somewhat obvious) law known as Amdahl's law, that essentially states that the improvement from parallel processing is determined by its slowest sequential component. Algorithms designed for this class of processor therefore require more care if they are not to unwittingly disrupt the potential gains.
Avoiding costs
- Defining variables as integers for indexed arrays instead of floating point will result in faster execution (see above).
- Defining structures whose structure length is a multiple of a power of 2 (2,4,8,16 etc.), will allow the compiler to calculate array indexes by shifting a binary index by 1, 2 or more bits to the left, instead of using a multiply instruction will result in faster execution. Adding an otherwise redundant short filler variable to 'pad out' the length of a structure element to say 8 bytes when otherwise it would have been 6 or 7 bytes may reduce overall processing time by a worthwhile amount for very large arrays. See[34] for generated code differences for C as for example.
- Storage defined in terms of bits, when bytes would suffice, may inadvertently involve extremely long path lengths involving bitwise operations instead of more efficient single instruction 'multiple byte' copy instructions. (This does not apply to 'genuine' intentional bitwise operations - used for example instead of multiplication or division by powers of 2 or for TRUE/FALSE flags.)
- Unnecessary use of allocated dynamic storage when static storage would suffice, can increase the processing overhead substantially - both increasing memory requirements and the associated allocation/deallocation path length overheads for each function call.
- Excessive use of function calls for very simple functions, rather than in-line statements, can also add substantially to instruction path lengths and stack/unstack overheads. For particularly time critical systems that are not also code size sensitive, automatic or manual inline expansion can reduce path length by eliminating all the instructions that call the function and return from it. (A conceptually similar method, loop unrolling, eliminates the instructions required to set up and terminate a loop by, instead; repeating the instructions inside the loop multiple times. This of course eliminates the branch back instruction but may also increase the size of the binary file or, in the case of JIT built code, dynamic memory. Also, care must be taken with this method, that re-calculating addresses for each statement within an unwound indexed loop is not more expensive than incrementing pointers within the former loop would have been. If absolute indexes are used in the generated (or manually created) unwound code, rather than variables, the code created may actually be able to avoid generated pointer arithmetic instructions altogether, using offsets instead).
- Memory management
- Whenever memory is automatically allocated (for example in HLL programs, when calling a procedure or when issuing a system call), it is normally released (or 'freed'/ 'deallocated'/ 'deleted' ) automatically when it is no longer required - thus allowing it to be re-used for another purpose immediately. Some memory management[35] can easily be accomplished by the compiler, as in this example. However, when memory is explicitly allocated (for example in OOP when "new" is specified for an object), releasing the memory is often left to an asynchronous 'garbage collector' which does not necessarily release the memory at the earliest opportunity (as well as consuming some additional CPU resources deciding if it can be). The current trend nevertheless appears to be towards taking full advantage of this fully automated method, despite the tradeoff in efficiency - because it is claimed that it makes programming easier. Some functional languages are known as 'lazy functional languages' because of their tendency to delay computations in form of allocated thunks, leading to significant use of garbage collection and can consume much more memory as a result.
- Array processing may simplify programming but use of separate statements to sum different elements of the same array(s) may produce code that is not easily optimized and that requires multiple passes of the arrays that might otherwise have been processed in a single pass. It may also duplicate data if array slicing is used, leading to increased memory usage and copying overhead.
- In OOP, if an object is known to be immutable, it can be copied simply by making a copy of a reference to it instead of copying the entire object. Because a reference (typically only the size of a pointer) is usually much smaller than the object itself, this results in memory savings and a boost in execution speed.
Readability, trade offs and trends
One must be careful, in the pursuit of good coding style, not to over-emphasize efficiency. Frequently, a clean, readable and 'usable' design is much more important than a fast, efficient design that is hard to understand. There are exceptions to this 'rule' (such as embedded systems, where space is tight, and processing power minimal) but these are rarer than one might expect.
However, increasingly, for many 'time critical' applications such as air line reservation systems, point-of-sale applications, ATMs (cash-point machines), Airline Guidance systems, Collision avoidance systems and numerous modern web based applications - operating in a real-time environment where speed of response is fundamental - there is little alternative.
Determining if optimization is worthwhile
The essential criteria for using optimized code are of course dependent upon the expected use of the algorithm. If it is a new algorithm and is going to be in use for many years and speed is relevant, it is worth spending some time designing the code to be as efficient as possible from the outset. If an existing algorithm is proving to be too slow or memory is becoming an issue, clearly something must be done to improve it.
For the average application, or for one-off applications, avoiding inefficient coding techniques and encouraging the compiler to optimize where possible may be sufficient.
One simple way (at least for mathematicians) to determine whether an optimization is worthwhile is as follows: Let the original time and space requirements (generally in Big-O notation) of the algorithm be 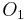 and
and 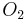 . Let the new code require
. Let the new code require 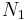 and
and 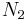 time and space respectively. If
time and space respectively. If 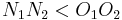 , the optimization should be carried out. However, as mentioned above, this may not always be true.
, the optimization should be carried out. However, as mentioned above, this may not always be true.
Implications for algorithmic efficiency
A recent report, published in December 2007, from Global Action Plan,[36] a UK-based environmental organisation found that computer servers are "at least as great a threat to the climate as SUVs or the global aviation industry" drawing attention to the carbon footprint of the IT industry in the UK.[37][38] According to an Environmental Research Letters report published in September 2008, "Total power used by information technology equipment in data centers represented about 0.5% of world electricity consumption in 2005. When cooling and auxiliary infrastructure are included, that figure is about 1%. The total data center power demand in 2005 is equivalent (in capacity terms) to about seventeen 1000 MW power plants for the world."[39]
Some media reports claim that performing two Google searches from a desktop computer can generate about the same amount of carbon dioxide as boiling a kettle for a cup of tea, according to new research;[40] however, the factual accuracy of this comparison is disputed,[41] and the author of the study in question asserts that the two-searches-tea-kettle statistic is a misreading of his work.[42]
Greentouch,[43][44] a recently established consortium of leading Information and Communications Technology (ICT) industry, academic and non-governmental research experts, has set itself the mission of reducing reduce energy consumption per user by a factor of 1000 from current levels. "A thousand-fold reduction is roughly equivalent to being able to power the world’s communications networks, including the Internet, for three years using the same amount of energy that it currently takes to run them for a single day". The first meeting in February 2010 will establish the organization’s five-year plan, first year deliverables and member roles and responsibilities. Intellectual property issues will be addressed and defined in the forum’s initial planning meetings. The conditions for research and the results of that research will be high priority for discussion in the initial phase of the research forum’s development.[45]
Computers having become increasingly more powerful over the past few decades, emphasis was on a 'brute force' mentality. This may have to be reconsidered in the light of these reports and more effort placed in future on reducing carbon footprints through optimization. It is a timely reminder that algorithmic efficiency is just another aspect of the more general thermodynamic efficiency. The genuine economic benefits of an optimized algorithm are, in any case, that more processing can be done for the same cost[46] or that useful results can be shown in a more timely manner and ultimately, acted upon sooner.
Criticism of the current state of programming
- David May FRS a British computer scientist and currently Professor of Computer Science at University of Bristol and founder and CTO of XMOS Semiconductor, believes one of the problems is that there is a reliance on Moore's law to solve inefficiencies. He has advanced an 'alternative' to Moore's law (May's law) stated as follows:[47]
He goes on to stateSoftware efficiency halves every 18 months, compensating Moore's Law
In ubiquitous systems, halving the instructions executed can double the battery life and big data sets bring big opportunities for better software and algorithms: Reducing the number of operations from N x N to N x log(N) has a dramatic effect when N is large... for N = 30 billion, this change is as good as 50 years of technology improvements
- Software author Adam N. Rosenburg in his blog "The failure of the Digital computer", has described the current state of programming as nearing the "Software event horizon", (alluding to the fictitious "shoe event horizon" described by Douglas Adams in his Hitchhiker's Guide to the Galaxy book[48]). He estimates there has been a 70 dB factor loss of productivity or "99.99999 percent, of its ability to deliver the goods", since the 1980s - "When Arthur C. Clarke compared the reality of computing in 2001 to the computer HAL in his book 2001: A Space Odyssey, he pointed out how wonderfully small and powerful computers were but how disappointing computer programming had become".
- Conrad Weisert gives examples, some of which were published in ACM SIGPLAN (Special Interest Group on Programming Languages) Notices, December 1995 in: "Atrocious Programming Thrives"[49]
- Marc Andreessen co-founder of Netscape is quoted in "Mavericks at Work" (ISBN 0060779616) as saying "Five great programmers can completely outperform 1,000 mediocre programmers."[5]
Managed code
For algorithms executing in a "managed code" environment (such as the .Net platform), there are many issues that impinge on performance. These [50][51] are links to two of them in the Microsoft .Net environment.
Competitions for the best algorithms
The following competitions invite entries for the best algorithms based on some arbitrary criteria decided by the judges:-
See also
- Arithmetic coding - a form of variable-length entropy encoding for efficient data compression
- Associative array - a data structure that can be made more efficient using Patricia trees or Judy arrays
- Binary search algorithm - a simple and efficient technique for searching sorted arrays
- Benchmark - a method for measuring comparative execution times in defined cases
- Best, worst and average case - considerations for estimating execution times in three scenarios
- Branch table - a technique for reducing instruction path-length, size of machine code, (and often also memory)
- Comparison of programming paradigms - paradigm specific performance considerations
- Compiler optimization - compiler-derived optimization
- Computational complexity theory
- Computer performance, - computer hardware metrics
- Data compression - reducing transmission bandwidth and disk storage
- Entropy encoding - encoding data efficiently using frequency of occurrence of strings as a criterion for substitution
- Garbage collection - automatic freeing of memory after use
- Green computing - a move to implement 'greener' technologies, consuming less resources
- Huffman algorithm - an algorithm for efficient data encoding
- Index (information technology) - a technique for fast lookup using indexes
- Locality of reference - for avoidance of caching delays caused by non-local memory access
- Loop optimization
- Memory management
- Optimization (computer science)
- Performance analysis – methods of measuring actual performance of an algorithm at run-time
- Real-time computing – further examples of time-critical applications
- Run-time analysis – estimation of expected run-times and an algorithm's scalability
- Super-threading
- Simultaneous multithreading
- Speculative execution or Eager execution
- Threaded code - similar to virtual method table or branch table
- Virtual method table - branch table with dynamically assigned pointers for dispatching
- Improving Managed code Performance - Microsoft MSDN Library
References
- ^ Breakdown occurs when an algorithm tries to compact itself. Success would solve the Halting problem.
- ^ http://pplab.snu.ac.kr/courses/adv_pl05/papers/p261-knuth.pdf
- ^ http://www-cs-faculty.stanford.edu/~knuth/.
- ^ "Google Doodles: 2011 October - December". Google.com. http://www.google.com/logos/. Retrieved 2011-12-14.
- ^ http://img0.gmodules.com/logos/olympics10-nordic-ig.gif
- ^ "Internet Users - Top 20 Countries - Internet Usage". Internetworldstats.com. http://www.internetworldstats.com/top20.htm. Retrieved 2011-12-14.
- ^ a b http://web.cecs.pdx.edu/~singh/ftp/infocom04.pdf
- ^ http://www.newscientist.com/article/mg20527435.400-worlds-communications-network-due-an-energy-diet.html dated 16/1/2010 page 15
- ^ http://www.scientificamerican.com/article.cfm?id=green-touch-launch dated 11/1/2010
- ^ "Green Touch: highlights of the press conference". YouTube. 2010-01-15. http://www.youtube.com/watch?v=huuLmjaz4Rw. Retrieved 2011-12-14.
- ^ "World Wide Web, Volume 10, Number 3". SpringerLink. http://www.springerlink.com/content/gv6q7541456g2540/. Retrieved 2011-12-14.
- ^ "Will binary XML solve XML performance woes?". Searchsoa.techtarget.com. http://searchsoa.techtarget.com/generic/0,295582,sid26_gci1050533,00.html. Retrieved 2011-12-14.
- ^ "i-Technology Viewpoint: The Performance Woe of Binary XML | SOA World Magazine". Soa.sys-con.com. http://soa.sys-con.com/node/250512. Retrieved 2011-12-14.
- ^ Frank Rubin published a criticism of Dijkstra's letter in the March 1987 CACM where it appeared under the title 'GOTO Considered Harmful' Considered Harmful. Frank Rubin (March 1987). ""GOTO Considered Harmful" Considered Harmful" (PDF). Communications of the ACM 30 (3): 195–196. doi:10.1145/214748.315722. http://www.ecn.purdue.edu/ParaMount/papers/rubin87goto.pdf.
- ^ "The AI Effect". Aaai.org. http://www.aaai.org/aitopics/html/aieffect.html. Retrieved 2011-12-14.
- ^ "An Interview with A. Stepanov". STLport. 1950-11-16. http://www.stlport.org/resources/StepanovUSA.html. Retrieved 2011-12-14.
- ^ "On the Tension Between Object-Oriented and Generic Programming in C". Artima.com. 2007-10-15. http://www.artima.com/cppsource/type_erasureP.html. Retrieved 2011-12-14.
- ^ * "Graphics Programming BlackBook" Chapter 7, pages 8 to 10
- ^ http://webhome.cs.uvic.ca/~nigelh/Publications/stringsearch.pdf
- ^ "IBM - Application Performance Analyzer for z/OS - Software". 306.ibm.com. http://www-306.ibm.com/software/awdtools/apa/. Retrieved 2011-12-14.
- ^ http://www.ics.uci.edu/~franz/Site/pubs-pdf/ICS-TR-07-12.pdf
- ^ "Whetstone Benchmark History". Roylongbottom.org.uk. http://www.roylongbottom.org.uk/whetstone.htm#anchorPC2. Retrieved 2011-12-14.
- ^ a b "Floating Point Benchmark: Comparing Languages (Fourmilog: None Dare Call It Reason)". Fourmilab.ch. 2005-08-04. http://www.fourmilab.ch/fourmilog/archives/2005-08/000567.html. Retrieved 2011-12-14.
- ^ "The Computer Language Benchmarks Game". Shootout.alioth.debian.org. http://shootout.alioth.debian.org/. Retrieved 2011-12-14.
- ^ http://www.osnews.com/story/5602
- ^ "Data Alignment Considerations". Msdn.microsoft.com. http://msdn.microsoft.com/en-us/library/aa505951.aspx. Retrieved 2011-12-14.
- ^ "Tips for Improving Time-Critical Code". Msdn.microsoft.com. http://msdn.microsoft.com/en-us/library/eye126ky.aspx. Retrieved 2011-12-14.
- ^ http://en.wikipedia.or/wiki/Subroutine#Optimization_of_subroutine_calls
- ^ a b c Guy Lewis Steele, Jr. "Debunking the 'Expensive Procedure Call' Myth, or, Procedure Call Implementations Considered Harmful, or, Lambda: The Ultimate GOTO". MIT AI Lab. AI Lab Memo AIM-443. October 1977. [1][2][3]
- ^ "The Java HotSpot Performance Engine: Method Inlining Example". Java.sun.com. 2002-08-13. http://java.sun.com/developer/technicalArticles/Networking/HotSpot/inlining.html. Retrieved 2011-12-14.
- ^ Surana P (2006) (PDF). Meta-Compilation of Language Abstractions.. ftp://lispnyc.org/meeting-assets/2007-02-13_pinku/SuranaThesis.pdf. Retrieved 2008-03-17.
- ^ Kuketayev. "The Data Abstraction Penalty (DAP) Benchmark for Small Objects in Java.". http://www.adtmag.com/joop/article.aspx?id=4597. Retrieved 2008-03-17.
- ^ Chatzigeorgiou; Stephanides (2002). "Evaluating Performance and Power Of Object-Oriented Vs. Procedural Programming Languages". In Blieberger; Strohmeier. Proceedings - 7th International Conference on Reliable Software Technologies - Ada-Europe'2002. Springer. p. 367.
- ^ "C to Assembly (For Loop, While Loop, Structure Access, Array Indexing)". Eventhelix.com. http://www.eventhelix.com/realtimemantra/Basics/CToAssemblyTranslation2.htm. Retrieved 2011-12-14.
- ^ "The Memory Management Reference". Memorymanagement.org. http://www.memorymanagement.org/. Retrieved 2011-12-14.
- ^ "Environmental Charity". Global Action Plan. http://www.globalactionplan.org.uk/. Retrieved 2011-12-14.
- ^ "Computer servers 'as bad' for climate as SUVs - environment - 03 December 2007 - New Scientist". Environment.newscientist.com. http://environment.newscientist.com/article/dn12992-computer-servers-as-bad-for-climate-as-suvs.html. Retrieved 2011-12-14.
- ^ "Innovators: Efficiency Matters - March April 2007 - Sierra Magazine". Sierra Club. http://www.sierraclub.org/sierra/200703/innovators.asp. Retrieved 2011-12-14.
- ^ "Worldwide electricity used in data centers". Iop.org. http://www.iop.org/EJ/article/1748-9326/3/3/034008/erl8_3_034008.html#erl280630s6. Retrieved 2011-12-14.
- ^ "Research Reveals Environmental Impact of Google Searches". Fox News. 2009-01-12. http://www.foxnews.com/story/0,2933,479127,00.html.
- ^ Timmer, John (2009-01-12). "Analysis: environmental impact of Googling hard to quantify". Arstechnica.com. http://arstechnica.com/news.ars/post/20090112-analysis-environmental-impact-of-googling-hard-to-quantify.html. Retrieved 2011-12-14.
- ^ "Technology News: Green Tech: Harvard Physicist Sets Record Straight on Internet Carbon Study". Technewsworld.com. http://www.technewsworld.com/rsstory/65794.html. Retrieved 2011-12-14.
- ^ "About Us". Green Touch. http://www.greentouch.org/index.php?page=about-us. Retrieved 2011-12-14.
- ^ "Gee Rittenhouse, Bell Labs, on Shannon's Law and the Green Touch initiative". YouTube. 2010-01-11. http://www.youtube.com/watch?v=VkymxXA2PeU&feature=player_embedded#!. Retrieved 2011-12-14.
- ^ "Challenges and Opportunities". Green Touch. http://www.greentouch.org/index.php?page=challenges-opportunities. Retrieved 2011-12-14.
- ^ "Energy Efficiency in the Data Center". YouTube. 2008-07-22. http://www.youtube.com/watch?v=2BfNGZiO4GU&feature=related. Retrieved 2011-12-14.
- ^ http://www.cs.bris.ac.uk/~dave/iee.pdf
- ^ http://www.the-adam.com/adam/rantrave/computers.htm
- ^ "Atrocious Programming Thrives". Idinews.com. 2003-01-09. http://www.idinews.com/atrocious.html. Retrieved 2011-12-14.
- ^ http://msdn.microsoft.com/en-us/library/ms973852
- ^ http://msdn.microsoft.com/en-us/library/ff647790.aspx
- ^ [4]
External links
- Animation of the Boyer-Moore algorithm (Java Applet)
- Programming Optimization by Paul Hsieh
- also see more external links in related article "program optimization"
- "Why learning assembler is still a good idea" By Randall Hyde
- Writing efficient programs ("Bentley's Rules") by Jon Bentley
- Why software still stinks" an article by Scott Rosenberg
- "In Defense of Efficient Computing" an article by Rod Furlan
- "Performance Anti-Patterns" by Bart Smaalders